![]()
Celebrating the
independent kiwi spirit of invention.
Research Topic: Six Sided Dice Roll Distribution
By Ian Mander BSc, 19 February 1999, updated 15 August 1999, updated 22 February 2013, updated 3 December 2014, updated 28 March 2023.
Question: How do you work out how many ways there are of making any particular number when throwing a given number of [six sided] dice?
Answer: With just one die, there are obviously six possible results. With each extra die added, each previous result has six new ways to be used. Therefore, one easy way to calculate the results is to use tables (such as a spreadsheet) to progressively sum for greater numbers of dice. The tables given below should be reasonably self-explanatory.
Each possible outcome total (for the number of dice being thrown – eg, you can throw anything from 2 to 12 inclusive for two dice) has a light blue background.
The number of ways of getting each outcome has a pale yellow background, and it's this line that's fed into the next table in six different positions for the six different ways the new die can be thrown.
Alternatively: This can also be calculated in a spreadsheet using a slightly complicated Pascal's triangle. Instead of summing just the two cells above it, each cell sums 6 cells above it. In other words, the cell above it and the 5 cells to that cell's left. This means allows only one row per die is required, not six plus the line of totals.
The outcome totals cannot be obtained directly from Pascal's Triangle. Although the leading diagonals start off well, they are inaccurate around the mean dice total. For example, the triangular numbers are found in the second diagonal and start 1, 3, 6, 10, 15, 21, 28, ...
Mathematically: The numbers of outcomes for each dice total are the coefficients of the expanded polynomial ( x + x2 + x3 + x4 + x5 + x6 )n where n is the number of dice rolled.
There are 6 terms in the brackets because we are talking about 6 sided dice – each die has 6 possible outcomes, which are represented by their exponents. The exponents of the individual terms in the expanded result also represent the outcome of the possible die rolls, because when we multiply a particular number which has different exponents, the exponents get added. This is handy, because we are adding the results on different dice.
So the results of one particular roll of 5, 6, and 6 would be represented like this:
⚄ + ⚅ + ⚅ = 17
x5 • x6 • x6 = x17
And the outcomes for 3 dice are 3 to 18:
( x + x2 + x3 + x4 + x5 + x6 )3 =
x3 + 3x4 + 6x5 + 10x6 + 15x7+ 21x8 + 25x9 + 27x10 + 27x11 + 25x12 + 21x13 + 15x14 + 10x15 + 6x16 + 3x17 + x18
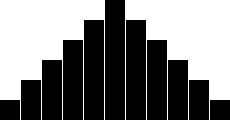
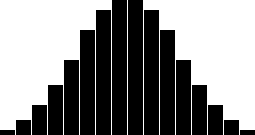
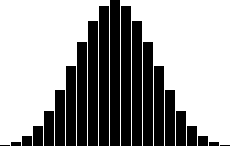
Observation: The more dice one throws at one time, the closer the result distribution approximates a normal distribution. As can be seen by the graphs below, anything from three dice upwards gives a reasonably close approximation to a normal distribution. However, the central peak gets narrower, so the standard deviation is getting smaller.
Wikipedia explains it thus:
... the central limit theorem ... states that, under mild conditions, the mean of a large number of random variables independently drawn from the same distribution is distributed approximately normally, irrespective of the form of the original distribution.
One die:
|
 |
Two dice:
|
 |
Three dice:
|
 |
Four dice:
|
 |
Update 28 March 2023:
Youtube channel 3Blue1Brown has a very well-made video about this which explains the background maths.
Celebrating the
independent kiwi spirit of invention.
Contact:
Return to ianman HOME | Back
to Aqualab Home | Return
to TOP
Inventions: Super
Soaker Backpack | Air
Cannon | Car
Interior Lighting | LED
Torch
* This would have been an ad. |
When you buy stuff from Asian sellers: |
| Please don't buy stuff from a country in the middle of intimidating its neighbours. | |
